Topological Phases
Topological phases of matter highlights the deep interplay of symmetry and topology and is stable under various local perturbations.
We study the entanglement scaling of 2+1 dimensional critical systems. Our main results include:
We developed a systematic approach to study the topological phases through analyzing the boundary gapless theory. Our main results include:
- The boundary gapless theory exhibits quantum anomaly if the bulk topological phase is protected by symmetry.
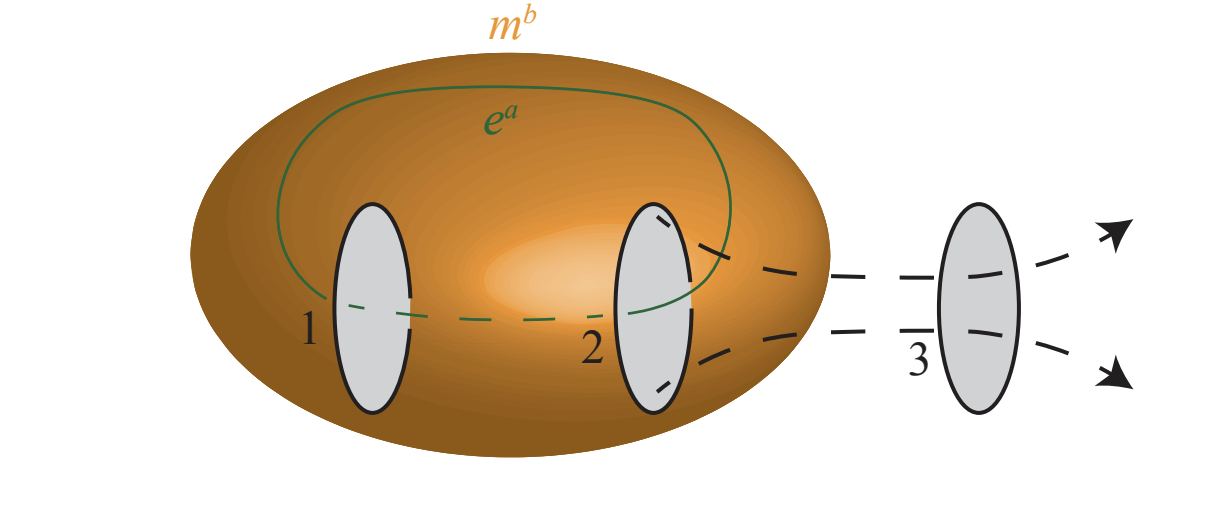
- By defining the appropriate boundary theory, we establish the bulk-boundary correspondence in a large class of 3+1 dimensional bosonic topological phases. We further analyze the possible braiding statistics of bulk topological excitations.
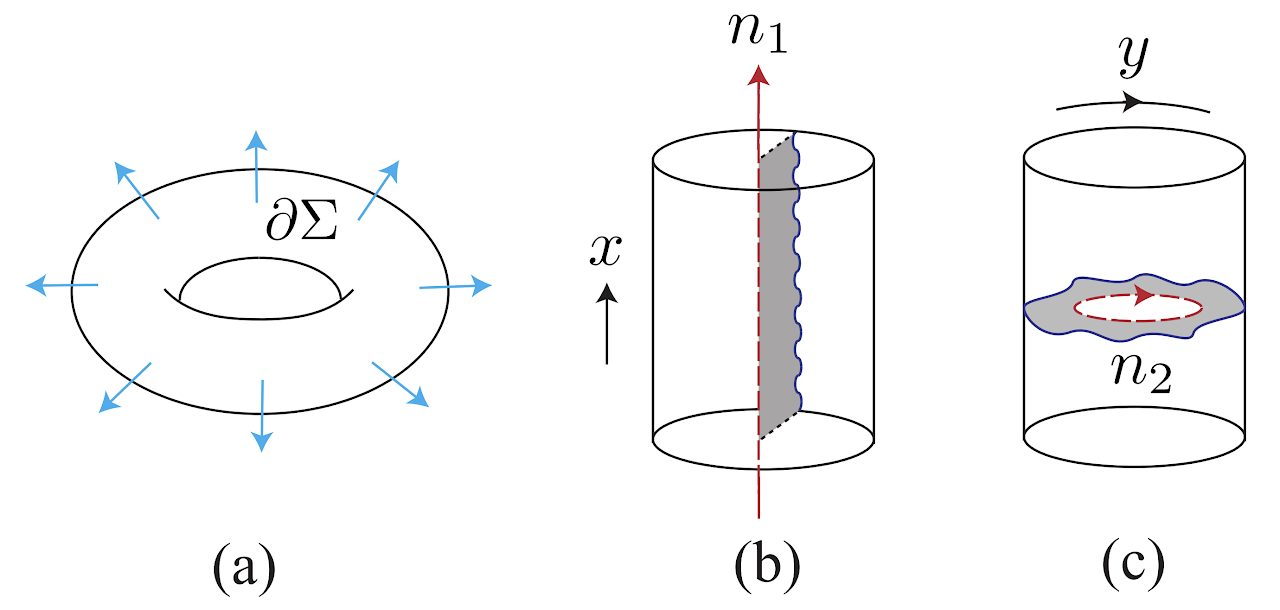
We introduce the twist defect in 2+1 dimensional topological phases and systematically study fusion and braiding statistics for it. This method can also help us construct more exotic non-abelian topological phases by introducing and proliferating symmetry defects in the parent topological phases.
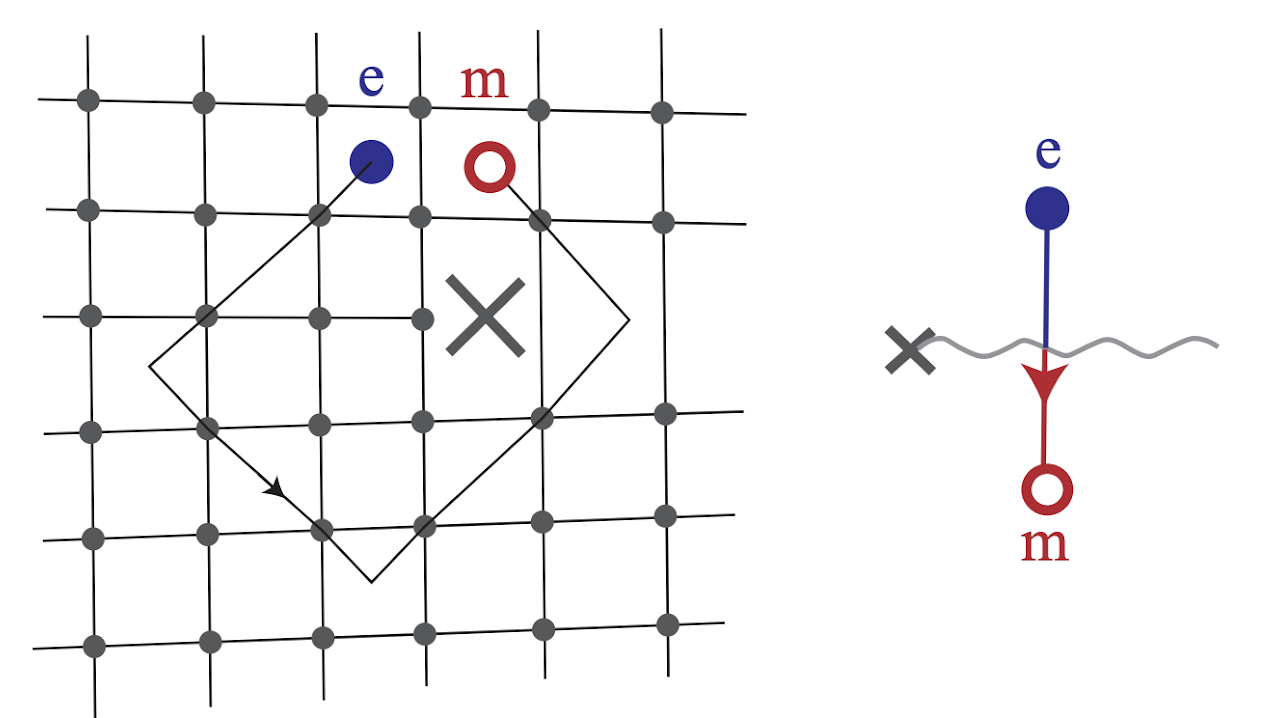
We use the twist defect to construct a series of 1+1 dimensional spin chain model and analyze the critical point described by the orbifold CFT.

We establish the connection between gauging symmetry in bulk topological phase and orbifolding symmetry in boundary gapless phase in 3+1 dimensions.